From neural activations to concepts: A survey on explaining concepts in neural
From neural activations to concepts: A survey on explaining concepts in neural networks
Background
- 人工智能的不可解释性
- 解释神经网络如何学习概念,因为概念可以作为构建复杂规则的原语
- 识别的概念可以帮助推理器干预神经网络,从而通过修改概念来调试网络
Neuron-level explanations
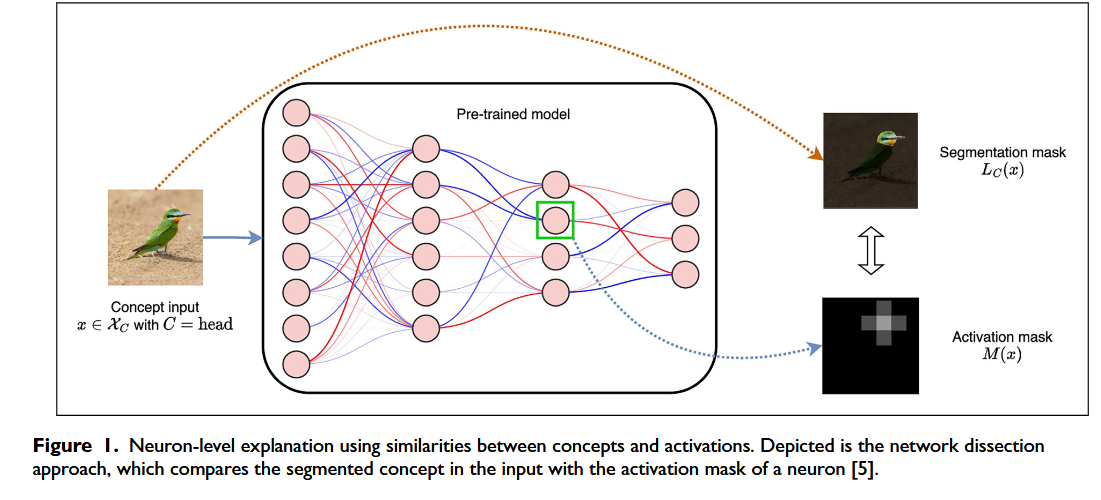
Using similarities between concepts and activations
- 使用概念和激活之间的相似性进行神经元级解释,用输入文字和图像得到激活图,最后与原始图像的mask进行对比,如果 IoU 值高于给定阈值,则卷积滤波器表示概念 C。

- 怀疑会不会不只是一个卷积滤波器表示一个概念,而是一些卷积滤波器的线性组合
- 利用CLIP, 因为CLIP 将图像和文本嵌入到同一矢量空间中,从而可以测量文本和图像之间的相似性,解释卷积滤波器所代表的概念,他们为滤波器选择一组激活度最高的图像,然后使用CLIP测量的图像与每个概念进行匹配,最后找到最匹配的概念。
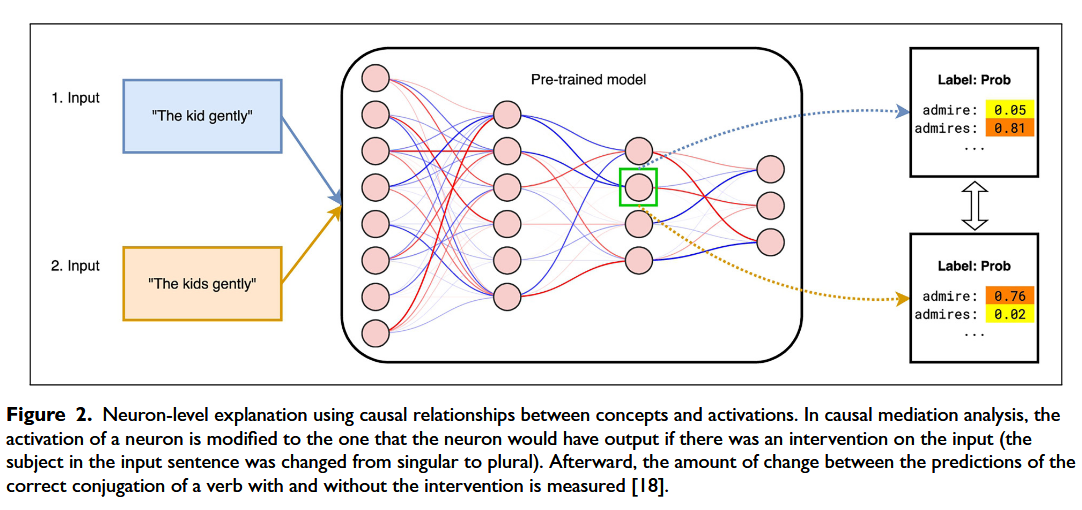
Using causal relationships between concepts and activations
- 分析通过干预输入和测量神经激活来展现输入概念和神经元之间的因果关系
方法1:将每个句子分解为一组连续的单词序列来提取概念,这些单词序列形成一个有意义的块。然后,通过首先重复概念以创建一个固定长度的合成句子(以规范不同概念的输入对单位的贡献),然后测量过滤器激活的平均值来衡量每个概念对过滤器激活的贡献。
方法2:首先将神经元的激活修改为在对输入进行干预时神经元将输出的激活(例如,输入句子中的主语从单数更改为复数),然后测量有和没有干预的动词正确变位预测之间的变化量
- GPT-2 中中间层前馈模块中的神经元与编码事实信息和实现权重修饰符以改变权重值和改变事实知识最相关。
Layer-level explanations
- 概念也可以用整层来表示,而不是神经元或卷积滤波器。
- 在层级解释中,有两种方法很突出:第一种是用概念激活向量进行解释,第二种是探测。两种方法之间的主要区别在于,线性二进制分类器是针对每个概念训练的;而在探测中,多类分类器是使用通常与某些语言特征(例如,情感,词性标签)相关的分类标签进行训练的。
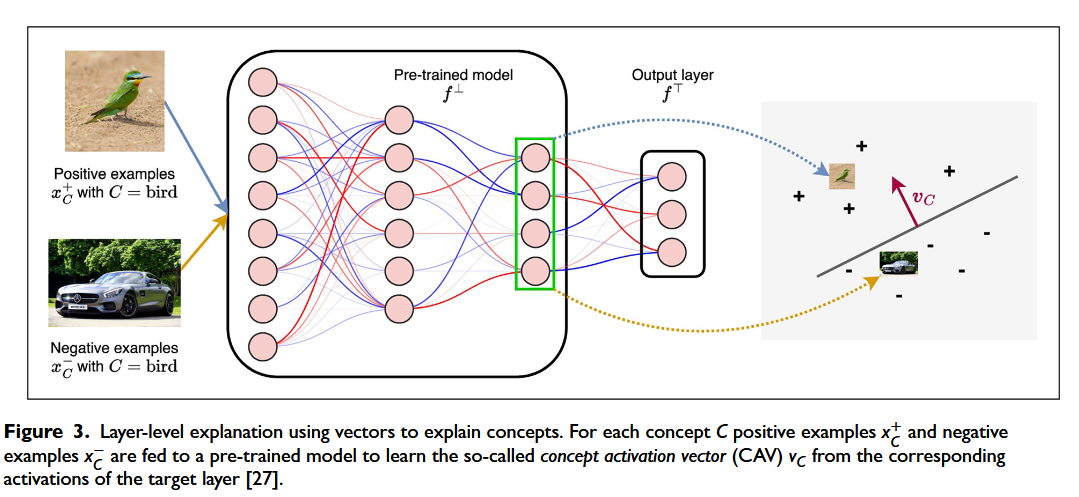
Using vectors to explain concepts: Concept activation vectors(概念激活向量)
概念激活向量(CAV),是一种用于神经网络层级概念解释的连续向量。其核心逻辑如下
1. 网络结构分解:
将神经网络 $f$ 拆分为两部分 $f = f^{\top} \circ f^{\perp}$,其中 $f^{\perp}: \mathbb{R}^m \rightarrow \mathbb{R}^n$ 是“底层网络”,包含我们感兴趣的卷积层 $l$;$f^{\top}$ 是“顶层输出层”。2. 概念识别流程:
为了识别某一概念 $C$(如“条纹”“鸟类”),需准备正例 $x_C^{+}$(含概念 $C$)和负例 $x_C^{-}$(不含概念 $C$)。将其输入 $f^{\perp}$ 后,收集对应激活 $f^{\perp}(x_C^{+}) \in \mathbb{R}^n$ 和 $f^{\perp}(x_C^{-}) \in \mathbb{R}^n$。
3. CAV 的生成:
训练一个线性分类器来区分 $f^{\perp}(x_C^{+})$ 和 $f^{\perp}(x_C^{-})$,该分类器决策边界的法向量 $v_C \in \mathbb{R}^n$ 即为概念 $C$ 的概念激活向量(CAV)。
CAV 的核心应用之一是测试输入与概念的相关性(TCAV, Testing with CAVs),用于衡量“概念 $C$ 对类别标签 $k$ 预测的影响程度”。其原理是:对数据集 $\mathcal{X}$ 中所有类别为 $k$ 的图像 $x$,将其潜在向量 $f^{\perp}(x)$ 沿 $v_C$ 方向移动(即 $f^{\perp}(x) + \varepsilon \cdot v_C$),观察 $f^{\top}$ 对标签 $k$ 的对数概率变化,以此量化概念 $C$ 对类别 $k$ 预测的“正影响概率”。
比如说:
假设我们想知道“鸟类特征($C$)对‘翠鸟类别($k$)’的预测有多大正影响”,过程如下:
步骤 1: 取所有真实类别为“翠鸟”的图像 $x$,即一批翠鸟的照片。
步骤 2: 对每个 $x$,计算其潜在向量 $f^{\perp}(x)$,得到这些翠鸟在“底层特征空间”中的表示。
步骤 3: 沿 $v_C$ 方向移动潜在向量,即计算 $f^{\perp}(x) + \varepsilon \cdot v_C$,相当于“为每张翠鸟图片添加更多‘鸟类共性特征’(如羽毛纹理、喙的形状等)”。
步骤 4: 将移动后的向量输入 $f^{\top}$,观察类别 $k$ 的对数概率。如果模型对“翠鸟($k$)”的对数概率上升,说明“注入鸟类特征后,模型更确信这是翠鸟”,即概念 $C$ 对类别 $k$ 有正影响。
步骤 5: 统计“正影响”的占比:在所有真实为翠鸟的图像中,计算满足“注入 $C$ 后对数概率上升”的样本比例,该比例即为“概念 $C$ 对类别 $k$ 的正影响概率”。
这一过程的本质是量化 “概念 C 的存在,多大程度上让模型更倾向于预测类别 k”。如果正影响概率很高,说明 “概念 C 是类别 k 的强特征”(比如 “鸟类特征” 对 “翠鸟” 分类的正影响概率很高);反之,则说明概念 C 对类别 k 的预测贡献很小。
- 问题:原 CAV 方法需手动准备 “带概念标签的图像数据集”,改进
- 无标签概念的自动生成
- 对同一类别的图像进行多分辨率分割,将分割后的 “区域簇” 作为 “隐式概念” 用于 TCAV
- 端到端的 CAV 与模型联合训练
- 不再单独准备概念数据集,而是在 “原始图像分类任务” 中同时训练 CAV 和模型。具体来说,计算 “向量值分数”(每个值对应一个可学习的概念,反映卷积层感受野中该概念的存在程度),并将分数输入多层感知机(MLP)完成分类,从而实现 “概念学习与分类任务的协同优化”。
- 无标签概念的自动生成
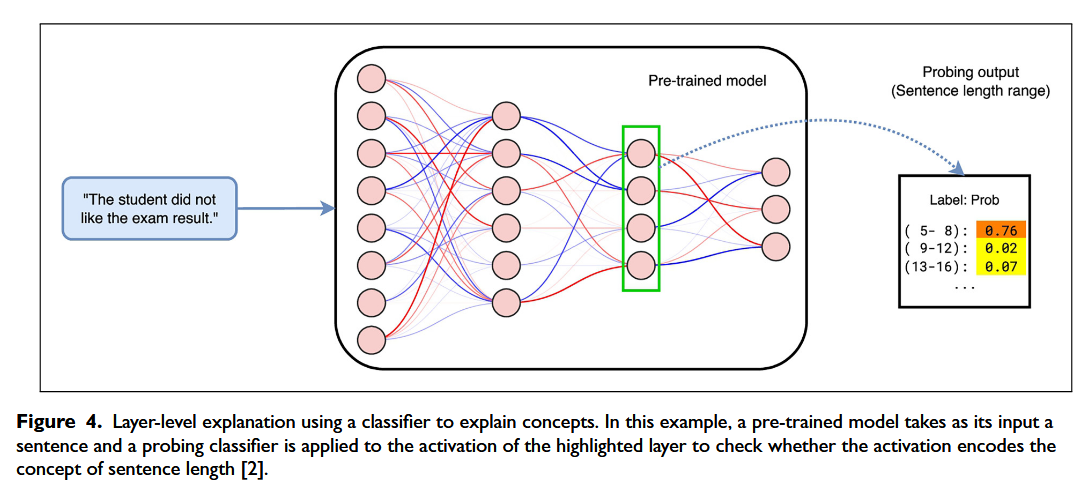
Using classifiers to explain concepts: Probing(探测)
- 探测使用分类器来解释概念。然而,探测不是为每个概念训练二进制线性分类器来测量概念在层激活中的存在,而是使用分类器进行多类分类
- 其标签通常代表 NLP 中的语言特征(例如,情感、词性标签)
Using localist representations: Concept bottleneck models (概念瓶颈模型)
每个概念都由模型f的瓶颈层中的一个唯一神经元表示
概念瓶颈模型(Concept Bottleneck Model, CBM)的整体结构可拆解为三个部分,通过函数组合($\circ$)构成完整模型 $f = f^{\top} \circ f_{l} \circ f^{\perp}$。各部分功能如下:
1. 底部模块($f^{\perp}$):
通常由预训练模型的底层构成,作用是从输入(如图片、文本)中提取基础特征。
2. 瓶颈层($f_{l}$):
作为核心模块,一般是一个线性层。它将 $f^{\perp}$ 提取的基础特征映射到“概念空间”,输出每个概念在当前输入中的强度(例如:“这张图中‘猫’的概念强度是 0.8,‘狗’是 0.1”)。
3. 顶部预测器($f^{\top}$):
接收瓶颈层输出的“概念强度”,并基于这些概念进行最终任务预测(如分类或回归)。
这种结构的优势在于可解释性——能够明确知道是哪些概念(如“有尾巴”“有胡须”)导致了模型的预测结果(如“这是猫”)。
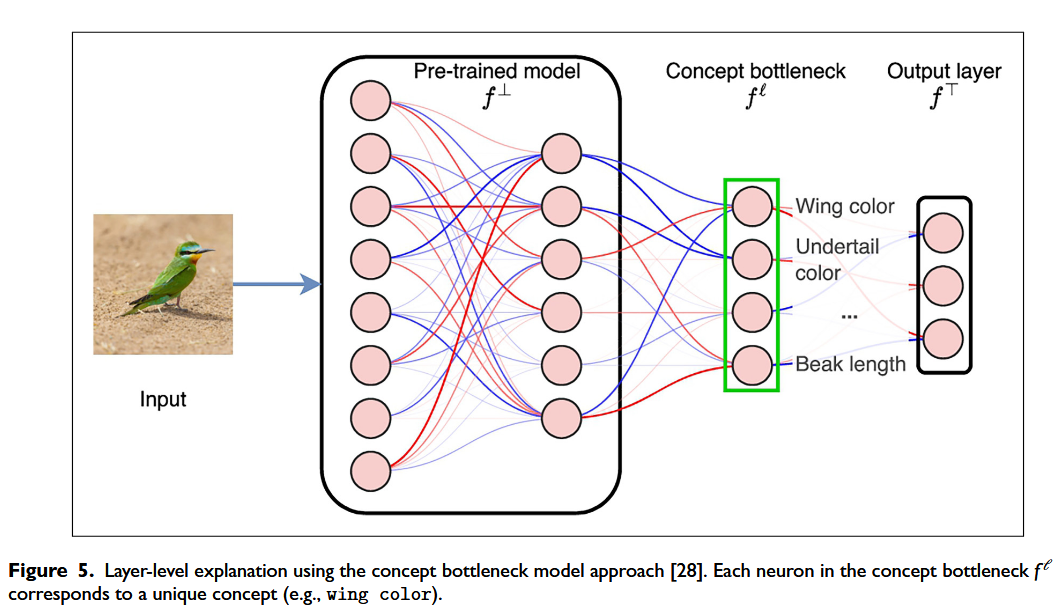
- 核心局限:训练瓶颈层时,除了任务标签(如 “这是猫”),还需要概念标签(如 “图中有尾巴、有胡须”)。但很多任务中,人工标注概念标签成本高或难以获取。
- 最新解决思路:无需人工标注概念标签,而是通过外部资源自动获取任务相关的概念集,具体步骤如下:
- 获取概念集,从外部资源中筛选与任务相关的概念,例如:
- 知识库;
- 常见词汇库(如 2 万个英文常用词);
- 大语言模型(如 GPT-3)生成的概念。
- 概念嵌入($v_C$):用 CLIP(一种视觉 - 语言模型)将每个概念词(如 “尾巴”“胡须”)转化为向量($v_C$)。
- 计算概念强度:通过计算 “输入特征(f⊥(x))” 与 “概念向量($v_C$)” 的余弦相似度,自动得到输入 x 中每个概念 C 的强度,替代人工标注的概念标签。
- 获取概念集,从外部资源中筛选与任务相关的概念,例如: